
再帰関数呼出し
「自分を呼ぶのに、ちゃんと終われる?─再帰のしくみを“呼び出しの流れ”でつかもう」
再帰関数呼出しは「同じ関数を、問題を小さくしながら呼ぶ」考え方
C言語の関数は、関数の中から 同じ関数 を呼び出せます。これが 再帰関数呼出し(recursive function call)です。
ここで大事なのは「自分自身を延々と呼ぶ」ではなく、
- 問題を少し小さくして
- 同じ関数を呼び
- いつか必ず止まる条件(基底条件)で終了する
という設計になっていることです。
再帰は、木構造や分割統治など「もともと再帰っぽい形をした問題」にすごく向いています。
一方で、何でも再帰にすると遅くなったり、スタックを使いすぎたりすることもあるので、使いどころを理解するのがポイントです。
再帰の考え方:再帰的定義(recursive definition)
再帰は「自分自身を使って定義できるもの」によく登場します。
再帰のイメージ(定義の形)
(1) ここが終点(基底条件)
(2) それ以外は、少し小さくして同じ形にする(再帰ステップ)
説明
再帰は必ず「終点(基底条件)」が必要です。これがないと永遠に呼び続けてしまいます。
サンプルプログラム
日常的で追いやすい例として、1 から n までの合計(1+2+…+n) を再帰で求めます。
プロジェクト名:chap8-9-1 ソースファイル名:chap8-9-1.c
Visual Studio でこのプログラムを実行するには、SDLチェック設定を変更しておく必要があります。
1.プロジェクト名を右クリックして、「プロパティ」をクリックします。
2.「C/C++」→「全般」→「SDLチェック」を「いいえ」に切り替えて「OK」をクリックします。
#include <stdio.h>
//--- 1 から n までの合計を返す(再帰) ---//
int sum_to(int n)
{
if (n > 0)
return n + sum_to(n - 1);
else
return 0;
}
int main(void)
{
int num;
printf("正の整数を入力してください:");
scanf("%d", &num);
printf("1から%dまでの合計は%dです。\n", num, sum_to(num));
return 0;
}実行例
正の整数を入力してください:4
1から4までの合計は10です。何が再帰なの?この関数の“2つの顔”
再帰関数には、だいたい必ずこの2要素があります。
再帰の2要素
| 要素 | 役割 | sum_to での例 |
|---|---|---|
| 基底条件 | ここまで来たら止める | n が 0 以下なら 0 を返す |
| 再帰ステップ | 問題を小さくして同じ関数へ | n + sum_to(n-1) |
表の説明
再帰は「止まる」「小さくする」がセットです。これが揃うと安心して読めます。
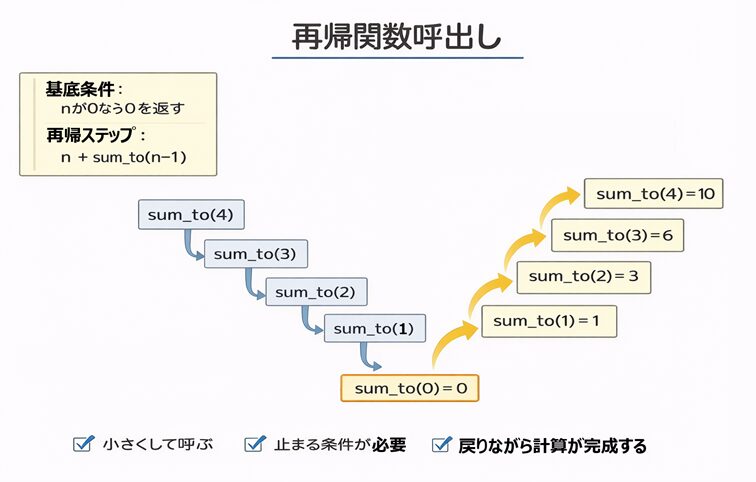
sum_to(4) はどう動く?
sum_to(4) を呼ぶと、内部では次のように呼び出しが連なります。
呼び出しが深くなる流れ(降りていく)
sum_to(4) → 4 + sum_to(3)
sum_to(3) → 3 + sum_to(2)
sum_to(2) → 2 + sum_to(1)
sum_to(1) → 1 + sum_to(0)
sum_to(0) → 0 (ここが基底条件)
説明
最初は「足し算を完了するために、下の結果が必要」なので、どんどん深く潜っていきます。
戻りながら計算が完成する(上っていく)
基底条件で 0 が返ると、そこから順に“戻りながら”計算が決まります。
返り値が積み上がる流れ(戻ってくる)
sum_to(0) = 0
sum_to(1) = 1 + 0 = 1
sum_to(2) = 2 + 1 = 3
sum_to(3) = 3 + 3 = 6
sum_to(4) = 4 + 6 = 10
説明
再帰は「呼び出しの階段を降りて、結果を持って階段を上る」感じです。
この“戻りながら完成する”のが、最初に混乱しやすいポイントです。
もう一歩:スタック(呼び出しの積み重なり)で見る
関数呼び出しは、内部で「未完了の仕事」が積まれていきます。
sum_to(4) のスタック的イメージ
| 段階 | いま積まれている仕事(イメージ) |
|---|---|
| sum_to(4) 呼び出し | 4 + (結果待ち) |
| sum_to(3) 呼び出し | 4 + (3 + 結果待ち) |
| sum_to(2) 呼び出し | 4 + (3 + (2 + 結果待ち)) |
| sum_to(1) 呼び出し | 4 + (3 + (2 + (1 + 結果待ち))) |
| sum_to(0) 到達 | 0 が確定→順に解決 |
表の説明
再帰が深くなるほど「結果待ちの仕事」が増えます。
これが “深すぎる再帰は危ない(スタックオーバーフロー)” にもつながります。
再帰が向く場面・向かない場面
「再帰なら何でもスッキリ!」とは限りません。向き不向きを整理します。
再帰の得意・不得意
| 観点 | 再帰が得意 | 再帰が苦手 |
|---|---|---|
| 問題の形 | 木・分割・入れ子構造 | 単純な繰り返し |
| コード | 短く書けることが多い | 逆に追いにくいことも |
| 実行 | 場合により効率的 | 呼び出しコストや深さが負担 |
| 例 | ディレクトリ探索、木の走査 | 1〜n 合計、階乗(学習向け) |
表の説明
今回の 1〜n 合計は「再帰の仕組みを学ぶ」には最高ですが、実務では for のほうが自然なことが多いです。
条件演算子で1行にする書き方(読みやすさは好み)
再帰関数は、条件演算子でも書けます。
return n > 0 ? n + sum_to(n - 1) : 0;
短くはなりますが、最初は if のほうが追いやすいことも多いです。
登場する命令・構文の書式と役割
関数定義の書式
戻り値の型 関数名(引数) { ... }
何をする?
処理をまとめ、呼び出せる形にします。再帰では「自分と同じ関数名」を本体で呼びます。
if の書式
if (条件)
文;
else
文;
何をする?
条件によって処理を分けます。再帰では基底条件(止まる条件)をここで作ることが多いです。
return の書式
return 式;
何をする?
関数の結果を呼び出し元へ返します。再帰では「戻りながら結果が完成する」ので超重要です。
printf / scanf の書式
- printf
printf("書式文字列", 値, ...); 表示します。 - scanf
scanf("書式文字列", 変数のアドレス, ...); 入力を読み取って変数へ入れます。
演習問題
演習8-6:sum_to を再帰を使わずに実装せよ
再帰なしで 1〜n の合計を返す関数を作成せよ。
解答例
int sum_to_loop(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++)
sum += i;
return sum;
}解説
- 単純な累積は for が自然
- 再帰より呼び出しコストがなく、深さの心配もありません
演習8-7:組合せ nCr を求める関数を作成せよ
次の定義を使って nCr を求める関数を作れ。
nCr = (n-1)C(r-1) + (n-1)Cr
ただし nC0 = nCn = 1、nC1 = n
解答例(再帰)
int combination(int n, int r)
{
if (r == 0 || r == n) return 1;
if (r == 1) return n;
return combination(n - 1, r - 1) + combination(n - 1, r);
}解説
- 定義そのものが再帰的なので、コードも素直に書けます
- ただし同じ計算が何度も出るので、n が大きいと遅くなりやすいです(メモ化で改善可能)
演習8-9:ユークリッドの互除法で最大公約数を求めよ
二つの整数 x と y の最大公約数を求める関数を作れ。
解答例(再帰)
int gcd(int x, int y)
{
if (y == 0) return x;
return gcd(y, x % y);
}解説
- 余りが 0 になったときが基底条件
- x % y の計算で問題サイズが小さくなるので、再帰と相性が良いです。
