
C言語基礎|符号付き整数の表現方式
同じ16ビットでも、負の並びが変わる!―2の補数・1の補数・符号と絶対値を“地図”で整理しよう。
符号付き整数は「負の作り方」が3通りある
符号無し整数は、ビット列をそのまま 0 から増えていく数として読めました。
でも 符号付き整数は、負の値をどう表すかで流派が分かれます。
C言語では、符号付き整数の内部表現として次の3方式が歴史的に存在し、どれを採用するかは処理系に委ねられています。
- 2の補数表現(two’s complement)
- 1の補数表現(one’s complement)
- 符号と絶対値表現(sign and magnitude)
ここで大事なのは、3方式とも ビット列そのもの(000…0 → 111…1 の並び)は同じなのに、
負側の値の割り当て(どのビット列が −5 なのかなど)が変わるという点です。
この記事では、まず「符号ビット」という共通ルールを押さえ、次に 3方式の値の範囲と並び方を表と図で整理していきます。
最後に、別のプログラム例で「同じビット列を3方式で読んだら値がどう変わるか」を実演しますね。

共通ルール:最上位ビットが符号ビット
3方式の共通点はこれです。
- 最上位ビット(いちばん左)が符号
- 0 なら非負(0または正)
- 1 なら負
図:符号ビットのイメージ(nビット)
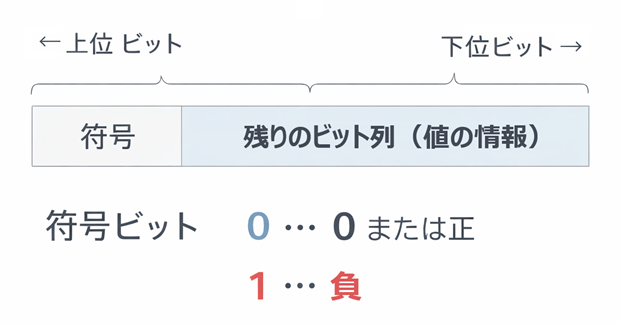
この図の説明
左端の1ビットが「プラスかマイナスか」を決めます。
ただし、符号ビット以外のビットの意味は方式によって変わります(ここが分かれ道です)。
3方式の特徴をまとめてつかむ
まずは「違いの全体像」を、短く表にします。
表:3方式の違い(まずは概要)
| 方式 | 0 の種類 | 負の並びのイメージ | 得意なこと |
|---|---|---|---|
| 2の補数 | 1種類 | 1000…0 が最小、111…1 が −1 | 加算・減算の回路が自然、主流 |
| 1の補数 | 2種類(+0 と −0) | 111…1 が −0、111…0 が −1 | 歴史的方式、今は珍しい |
| 符号と絶対値 | 2種類(+0 と −0) | 符号だけ立てて絶対値を保持 | 人間には直感的、計算は面倒 |
この表の説明
- 2の補数だけが 0が1種類なのでルールがすっきりします。
- 1の補数と符号と絶対値は −0が登場しやすく、扱いがややこしくなりがちです。
- 現代環境で2の補数が多いのは、計算が作りやすいのが大きな理由です。
表現できる値の範囲(nビットでの一般式)
ユーザー提示の本文にある範囲を、読みやすく整理します。
nビット符号付き整数の表現範囲(一般式)
| 方式 | 最小値 | 最大値 | 種類数 |
|---|---|---|---|
| 2の補数 | −2(n−1) | 2(n−1) − 1 | 2n |
| 1の補数 | −(2(n−1) − 1) | 2(n−1) − 1 | 2n − 1 |
| 符号と絶対値 | −(2(n−1) − 1) | 2(n−1) − 1 | 2n − 1 |
この表の説明
- 2の補数は負側が 1個多く表現でき、合計 2n 種類をきっちり使えます。
- 1の補数と符号と絶対値は、+0 と −0 のような重複が生まれやすく、合計が1つ少なくなります。
具体例:8/16/32/64ビットの範囲
符号付き整数型の表現範囲の一例(2の補数)
| ビット数 | 最小値 | 最大値 |
|---|---|---|
| 8 | −128 | 127 |
| 16 | −32768 | 32767 |
| 32 | −2147483648 | 2147483647 |
| 64 | −9223372036854775808 | 9223372036854775807 |
符号付き整数型の表現範囲の一例(1の補数/符号と絶対値)
| ビット数 | 最小値 | 最大値 |
|---|---|---|
| 8 | −127 | 127 |
| 16 | −32767 | 32767 |
| 32 | −2147483647 | 2147483647 |
| 64 | −9223372036854775807 | 9223372036854775807 |
この2つの表の説明
- 16ビットで見ると、2の補数は −32768 まで行ける。
- 1の補数/符号と絶対値は −32767 が下限(負側が1つ少ない)
- ここが「2の補数は 0 が1種類」の効果でもあります。
16ビットの符号付き整数の値と内部表現のビット
ポイントは2つです。
- 0 と正の内部表現は、3方式で共通
つまり、符号ビットが 0 の範囲は、符号無し整数の読み方と同じ感覚でOKです。 - 負の内部表現だけが方式ごとに変わる
符号ビットが 1 の範囲で、どのビット列がどの負数になるかが変わります。
さらに注意点として、
- 1の補数と符号と絶対値には −0 が登場する。
- その −0 のビットパターンを「数値の −0 として扱うかどうか」も処理系差があり得る。
- なので、実務では −0 のパターンに依存した表現は避けるのが安全です。
サンプルプログラム
同じ16ビットのビット列を、3方式それぞれで「値として読む」プログラムです。
プロジェクト名:chap7-15-1 ソースファイル名:chap7-15-1.c
// 同じビット列を、3方式(2の補数 / 1の補数 / 符号と絶対値)で値に解釈して表示する
#include <stdio.h>
unsigned to_unsigned16(unsigned x)
{
return x & 0xFFFFu;
}
int value_twos_complement(unsigned bits)
{
// 16ビット2の補数として解釈
bits = to_unsigned16(bits);
if (bits & 0x8000u) {
return (int)(bits - 0x10000u); // 2^16 を引く
}
return (int)bits;
}
int value_ones_complement(unsigned bits)
{
// 16ビット1の補数として解釈(-0 も存在しうる)
bits = to_unsigned16(bits);
if (bits & 0x8000u) {
unsigned mag = (~bits) & 0xFFFFu; // 全反転した絶対値
if (mag == 0u) return 0; // -0 は 0 として表示(扱いは処理系差があり得る)
return -(int)mag;
}
return (int)bits;
}
int value_sign_magnitude(unsigned bits)
{
// 16ビット符号と絶対値として解釈(-0 も存在しうる)
bits = to_unsigned16(bits);
unsigned mag = bits & 0x7FFFu;
if (bits & 0x8000u) {
if (mag == 0u) return 0; // -0 は 0 として表示
return -(int)mag;
}
return (int)mag;
}
int main(void)
{
// 例:ビット列 0x8001(1000 0000 0000 0001)
// 2の補数だと -32767、1の補数や符号と絶対値だと -1 の系列に近い振る舞いになる
unsigned bits = 0x8001u;
puts("同じ16ビットの並びでも、表現方式が違うと値が変わります。");
printf("対象ビット列 = 0x%04X\n", bits);
printf("2の補数として読む : %d\n", value_twos_complement(bits));
printf("1の補数として読む : %d\n", value_ones_complement(bits));
printf("符号と絶対値として読む : %d\n", value_sign_magnitude(bits));
return 0;
}実行結果例(例なので環境に依存しない)
同じ16ビットの並びでも、表現方式が違うと値が変わります。
対象ビット列 = 0x8001
2の補数として読む : -32767
1の補数として読む : -32766
符号と絶対値として読む : -1この結果の説明
- 同じ 0x8001 でも、方式で読み方が変わります。
- だから 「負側の並びが方式ごとに違う」という話につながります。
- なお、現実のC処理系は通常2の補数なので、実際の int の内部表現としては 2の補数が前提になりやすいです(ただし規格上は処理系依存)
登場する命令(関数・演算子)の書式と役割
今回出てきた「命令」を、学習用に整理します。
puts
| 項目 | 内容 |
|---|---|
| 書式 | puts(文字列); |
| 何をする? | 文字列を表示して改行も出す |
printf
| 項目 | 内容 |
|---|---|
| 書式 | printf(書式文字列, 値, ...); |
| 何をする? | 書式に従って値を表示する(例:%d は int、%04X は16進4桁表示) |
ビット演算とマスク
| 演算子 | 書式 | 何をする? | この記事での使い方 |
|---|---|---|---|
| & | a & b | 共通して1のビットだけ残す | 16ビットに切り詰める、符号ビット判定 |
| ~ | ~a | 全ビット反転 | 1の補数の絶対値を作る |
| - | a - b | 減算 | 2の補数の負数を作るため 2^16 を引く |
まとめ(ここで押さえるべき要点)
- 符号付き整数の表現方式は 2の補数 / 1の補数 / 符号と絶対値 の3つ
- 符号ビットは共通(最上位ビットが 0 なら非負、1 なら負)
- 0と正の並びは共通、違うのは 負の割り当て
- 1の補数と符号と絶対値では −0 が登場し、扱いも注意が必要
- 現代の主流は 2の補数(計算がすっきり)
