
C言語基礎|符号付き整数の内部表現
符号ビットは同じ。でも“負の作り方”が3通りある!――ビット列を読めると、Cの整数が急に分かりやすくなる。
符号付き整数の箱の中をのぞいてみよう
符号無し整数は「2進数をそのままビットに並べる」だけでした。
でも **符号付き整数(負の数を扱える整数)**になると話がちょっと増えます。
というのも、負の数をビット列で表す方法が、昔から代表的に3種類あるからです。
- 符号と絶対値表現(sign and magnitude)
- 1の補数表現(one’s complement)
- 2の補数表現(two’s complement)
そしてC言語の規格上、どれを採用するかは処理系(コンパイラやCPUなど)に委ねられています。
ただ、現代の多くの環境では 2の補数が主流です。
この記事ではまず、3方式の共通点である 符号ビットから入り、
次に「同じビット列でも方式によって値が変わる」ポイントを、表と図でしっかり整理していきます。
まず共通点:最上位ビットが符号ビット
符号付き整数の3方式に共通している考え方はこれです。
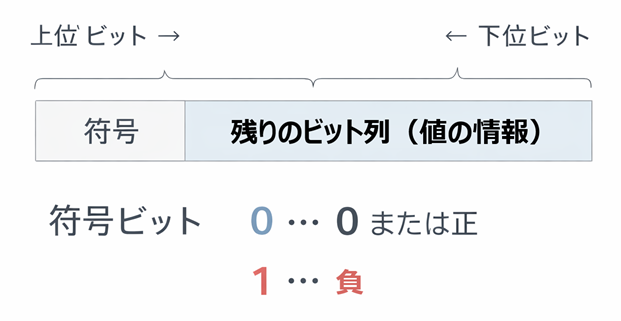
- 最上位ビット(いちばん左)で符号を表す
- 符号ビットが 0 なら非負(0または正)
- 符号ビットが 1 なら負
図:符号付き整数の符号ビット(イメージ)
この図の説明
箱の左端(最上位)が「プラスかマイナスか」を決めます。
ただし 残りのビット列が何を意味するかが、方式によって変わります。
3方式の違い:負の値の作り方が違う
ここでは分かりやすく 8ビットで例を出します(短いので目で追いやすいです)。
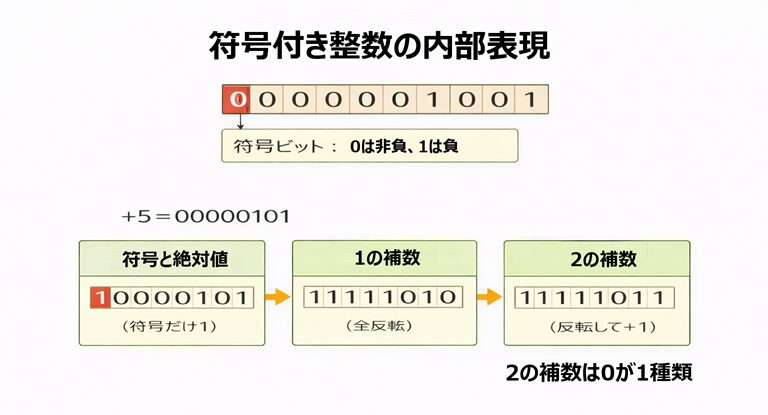
例:+5 のビット列(8ビット)
+5 は 00000101
ここから −5 を作るとき、方式によってこう変わります。
+5 から −5 を作るルール(8ビット例)
| 方式 | ルール(正のビット列から) | −5 のビット列(8ビット) | 重要ポイント |
|---|---|---|---|
| 符号と絶対値 | 符号ビットだけ 0→1、他はそのまま | 10000101 | 直感的だが 0 が2種類になりやすい |
| 1の補数 | 全ビット反転 | 11111010 | これも 0 が2種類になりやすい |
| 2の補数 | 1の補数を作って 1 を足す | 11111011 | 0 が1種類、計算がやりやすい |
この表の説明
- 3方式とも「符号ビットは1で負」を使います。
- でも「負の中身(残りのビット列)」の作り方が違います。
- 特に 2の補数は 反転+1 が合言葉です。
“同じビット列の並び”を、方式ごとにどう読む?
次は「ビット列の並び(00000000 から 11111111 まで)」を方式ごとに読むとどうなるか、ざっくり掴みます。
図:8ビットのビット列は同じ順番で並ぶ

この図の説明
ビット列の“並び”は、方式が違っても同じです。
違うのは「そのビット列に割り当てられる数値」です。特に負側が変わります。
0 が何種類あるかが、方式のクセを決める
3方式を比べると、学習者がいちばん納得しやすい差はここです。
0 の扱いの違い
| 方式 | 0 の種類 | 例(8ビット) | 影響 |
|---|---|---|---|
| 符号と絶対値 | 2種類 | +0 = 00000000 −0 = 10000000 | 比較や計算でルールが増えがち |
| 1の補数 | 2種類 | +0 = 00000000 −0 = 11111111 | 同上 |
| 2の補数 | 1種類 | 0 = 00000000 のみ | ルールがすっきり、計算に強い |
この表の説明
0 が2種類あると「0なのに違うビット列」が登場します。
2の補数はそれが起きないので、演算回路や言語処理の都合が良い、という流れです。
表現できる範囲(8ビット例でイメージ)
ビット数が同じでも、方式で表現範囲が少し変わります。
8ビット符号付き整数の範囲(方式別)
| 方式 | 最小値 | 最大値 |
|---|---|---|
| 符号と絶対値 | −127 | +127 |
| 1の補数 | −127 | +127 |
| 2の補数 | −128 | +127 |
この表の説明
- 2の補数は負側が 1つ多く表現できます(−128 まで行ける)
- これは「負側の作り方」が反転+1になっている結果です。
サンプルプログラム
ここでは +42 を例にして、
「3方式の負のビット列」を計算で作って表示します。
※これは「その処理系がどの方式か」を断定するプログラムではなく、3方式のルールを見える化するためのプログラムです。
プロジェクト名:chap7-14-1 ソースファイル名:chap7-14-1.c
// 符号付き整数の3方式(符号と絶対値 / 1の補数 / 2の補数)のビット列を作って表示する
#include <stdio.h>
void print_bits_u8(unsigned char v)
{
for (int i = 7; i >= 0; i--) {
putchar((v & (1u << i)) ? '1' : '0');
}
}
int main(void)
{
unsigned char p = 42; // +42(0〜127を想定して例にする)
unsigned char sign_mag = p | 0x80; // 符号と絶対値:符号ビットを1にする
unsigned char ones = (unsigned char)~p; // 1の補数:全ビット反転
unsigned char twos = (unsigned char)(ones + 1u); // 2の補数:反転して +1
puts("正の値から、負のビット列を3方式で作ってみよう(8ビット表示)");
printf("+42 : ");
print_bits_u8(p);
putchar('\n');
printf("符号と絶対値での -42: ");
print_bits_u8(sign_mag);
putchar('\n');
printf("1の補数での -42 : ");
print_bits_u8(ones);
putchar('\n');
printf("2の補数での -42 : ");
print_bits_u8(twos);
putchar('\n');
return 0;
}実行結果例
正の値から、負のビット列を3方式で作ってみよう(8ビット表示)
+42 : 00101010
符号と絶対値での -42: 10101010
1の補数での -42 : 11010101
2の補数での -42 : 11010110この出力の説明
- 00101010 が +42
- 方式ごとに「負の作り方」が違うので、ビット列も全部変わります
- 2の補数は 1の補数に 1 を足したものになっています
登場する命令(関数・演算子)の書式と役割
ここでは「この記事で使ったもの」が何をするのかを、ちゃんと整理しますね。
puts
| 項目 | 内容 |
|---|---|
| 書式 | puts(文字列); |
| 何をする? | 文字列を表示して、最後に改行も出す |
printf
| 項目 | 内容 |
|---|---|
| 書式 | printf(書式文字列, 値, ...); |
| 何をする? | 書式に合わせて値を表示する |
putchar
| 項目 | 内容 |
|---|---|
| 書式 | putchar(文字); |
| 何をする? | 1文字だけ出力する(ここでは 0 と 1 を1個ずつ表示) |
ビット演算(今回の主役)
| 演算子 | 書式 | 何をする? | この記事での使い方 |
|---|---|---|---|
| & | a & b | 両方1のビットだけ1 | 指定したビットが1か確認 |
| | | a | b | どちらか1なら1 | 符号ビットを立てる(0x80 を足すイメージ) |
| ~ | ~a | 全ビット反転 | 1の補数を作る。 |
| << | 1u << i | 1を左へ i ずらす | i番目のビットだけ立ったマスクを作る。 |
| + | a + 1u | 加算 | 2の補数の 反転+1 の 1 を足す。 |
ここまでのまとめ
- 符号付き整数の内部表現は 3方式(符号と絶対値 / 1の補数 / 2の補数)
- 共通点は「最上位ビットが符号」
- 違いは「負のとき、残りのビット列が何を意味するか」
- 2の補数は 0が1種類で計算が得意(現代の主流になりやすい)
次の学習では、この「2の補数の読み方」を使って、負の値をビット列から逆算したり、オーバーフローの感覚を掴んだりしていけます。
