
C言語基礎|負値のビット構成の求め方
マイナスの正体は“ビットのひと工夫”!反転+1が分かると、符号付き整数が一気にクリアになる。
負の数って、ビットではどう表すの?
10進数で −5 みたいな負の数、私たちは当たり前に使ってますよね。
でもコンピュータの中身は 0 と 1 だけ。じゃあ マイナスはどうやって表すの?…っていうのが今回のテーマです。
この記事では「正の数のビット列」からスタートして、対応する「負の数のビット列」を作る手順を学びます。
そしてその表し方には、代表的に次の 3種類があります。
- 符号と絶対値(Sign and Magnitude)
- 1の補数(One’s Complement)
- 2の補数(Two’s Complement)
特に大事なのは、現代のほとんどのCPUで採用されているのが 2の補数だという点です。
だから、最後に「反転して +1」の意味が腹落ちすると、符号付き整数が一気に読みやすくなります。
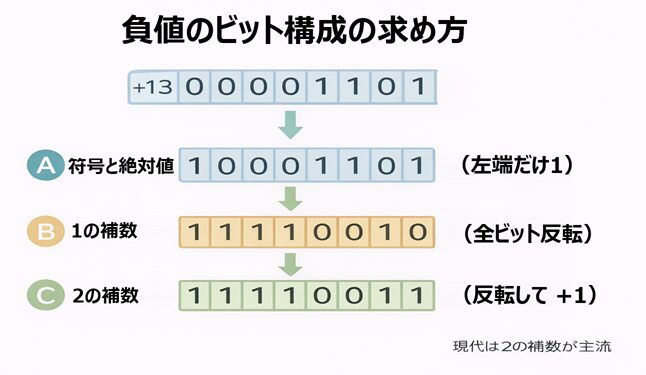
まず全体像:正値 → 負値の作り方(3方式まとめ)
ここでは分かりやすく、8ビットで例を作ります(図が短くて読みやすいので)。
正値として +13 を使い、そこから −13 を作ります。
図:+13 の 8ビット表現
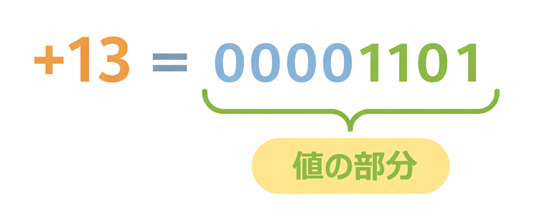
表:+13 → −13 の変換ルール
| 方式 | 変換のやり方(正値のビット列から) | −13 の結果(8ビット例) | 特徴 |
|---|---|---|---|
| 符号と絶対値 | 符号ビット(最上位)だけ 0→1 にする | 10001101 | 直感的だけど 0 が2種類になりやすい |
| 1の補数 | 全ビットを反転(0↔1) | 11110010 | これも 0 が2種類になりやすい |
| 2の補数 | 1の補数を作って 1 を足す | 11110011 | 0 が1種類で扱いやすく、現代の主流 |
この表の説明
- 「符号と絶対値」は“符号だけ別で持つ”発想
- 「1の補数」は“全ビット反転”というシンプル変換
- 「2の補数」は“反転+1”で、計算機にとって都合が良い仕組み
A:符号と絶対値(符号ビットをひっくり返す)
ルール
- 最上位ビット(符号ビット)だけを 1 にする。
- それ以外は正の数と同じ。
図:+13 → −13(符号と絶対値)

つまずきポイント(やさしく注意)
この方式は直感的なんですが、+0 と −0 が両方存在しやすいのが弱点です。
「0 なのに2種類ある」と、比較や計算のルールが面倒になりがちです。
B:1の補数(全ビット反転)
ルール
- 0 は 1 に、1 は 0 にする(ビット反転)
図:+13 → −13(1の補数)

つまずきポイント
これも +0(00000000) を反転すると 11111111(−0) のようになり、
やっぱり 0 が2種類問題が出やすいです。
C:2の補数(1の補数に 1 を足す)
ルール
- まず 1の補数(全反転)を作る。
- そこに 1 を加える。
図:+13 → −13(2の補数)

この図の説明
- 反転で“ひっくり返した世界”を作って
- 最後に +1 することで、0 の扱いがきれいに整います
なぜ 2の補数が便利なの?
一番うれしいのはこれです。
- 足し算の回路がそのまま引き算にも使える
たとえば「a − b」は「a + (−b)」で計算できます。
−b を 2の補数で作れれば、あとは普通に足すだけでOK。計算機的にとても相性が良いんです。
どの方式が使われているの?
実務・現代のCPUの世界では、ほぼ 2の補数が主流です。
なので学習のゴールとしては、
- 2の補数で負値を作れる
- 2の補数のビット列を見て「だいたいこのくらいの値かな」が分かる
ここまで行けるとめちゃ強いです。
サンプルプログラム
ここでは +13 → −13 を、プログラムで 8ビットの見た目として確認します。
プロジェクト名:chap7-13-1 ソースファイル名:chap7-13-1.c
// 正の数から負の数のビット列を作って確認する(8ビット表示)
#include <stdio.h>
void print_bits_u8(unsigned char v)
{
for (int i = 7; i >= 0; i--) {
putchar((v & (1u << i)) ? '1' : '0');
}
}
int main(void)
{
signed char p = 13; // +13
signed char n = (signed char)(-p); // -13(処理系の表現に従う)
puts("プラスとマイナスのビットを見比べてみよう(8ビット表示)");
printf("+13 のビット: ");
print_bits_u8((unsigned char)p);
putchar('\n');
printf("-13 のビット: ");
print_bits_u8((unsigned char)n);
putchar('\n');
return 0;
}実行結果例(2の補数の処理系ならこうなることが多い)
プラスとマイナスのビットを見比べてみよう(8ビット表示)
+13 のビット: 00001101
-13 のビット: 11110011※ 注意:C言語として「符号付き整数が必ず2の補数」とは規格で固定されていません。ただし現代環境では 2の補数が一般的です。
登場する命令(関数・演算子)の書式と役割
puts(関数)
| 項目 | 内容 |
|---|---|
| 書式 | puts(文字列); |
| 何をする? | 文字列を表示して最後に改行も出す |
printf(関数)
| 項目 | 内容 |
|---|---|
| 書式 | printf(書式文字列, 値, ...); |
| 何をする? | 書式に合わせて表示する |
putchar(関数)
| 項目 | 内容 |
|---|---|
| 書式 | putchar(文字); |
| 何をする? | 1文字出力する(ここでは 0 と 1 の表示に使用) |
キャスト(型変換)
| 項目 | 内容 |
|---|---|
| 書式 | (型名) 式 |
| 何をする? | 値をその型として扱う |
| この記事での役割 | signed char を unsigned char として見て、ビット列をそのまま表示する |
& と <<(ビット演算)
| 演算子 | 書式 | 何をする? | この記事での役割 |
|---|---|---|---|
| & | a & b | 同じ桁が1のときだけ1 | 特定ビットが立ってるか判定 |
| << | 1u << i | 1 を左へ i ずらす | チェック用マスク作成 |
まとめ:負値ビットは「ルール」で作れる
- 符号と絶対値:符号ビットだけ変える。
- 1の補数:全部反転
- 2の補数:全部反転して +1(現代の主流)
正のビット列から負のビット列を作る手順は、ほんとに機械的でシンプル。
「反転+1」が自然に手でできるようになると、次の学習(オーバーフロー、符号拡張、ビット演算)がすごく楽になります。
