
C言語基礎|ビット演算とシフト演算の応用
ビットは“小さなスイッチ”。AND/OR/XOR とシフトを組み合わせれば、自由自在にON/OFFできる!
ここまでで、ビット単位の論理演算子(& / | / ^ / ~)と、シフト演算子(<< / >>)をひととおり学びました。
この序章では、それらを「知っている」から一歩進んで、使って役に立つ形にするのが目標です。
たとえば現場では、こんなことをよくやります。
- ある設定フラグだけを 1 にする(セット)
- ある設定フラグだけを 0 にする(リセット)
- ある設定フラグだけを反転する(トグル)
- 1 の個数(セットされたビット数)を数える(ビットカウント)
- ビット列を回転させる(ローテート)
これらは、ビット演算 + シフト演算の組み合わせで作れます。
そのために、まずは提示文に出てくる3つの関数(count_bits / int_bits / print_bits)の意味を、図と表でしっかり整理していきましょう。
この記事で登場する演算子と「何をする命令か」
まずは道具一覧です。ビット演算は「ビット単位での処理」、シフトは「位置ずらし」です。
ビット演算子(論理演算)と役割
| 演算子 | 書式 | 何をする命令? | よく使う用途 |
|---|---|---|---|
| & | a & b | a と b の各ビットで AND(両方1なら1) | 特定ビットだけ抜き出す、0にする |
| | | a | b | a と b の各ビットで OR(一方1なら1) | 特定ビットを1にする(セット) |
| ^ | a ^ b | a と b の各ビットで XOR(片方だけ1なら1) | 特定ビットを反転(トグル) |
| ~ | ~a | a の全ビットを反転 | マスク作成、反転 |
シフト演算子と役割
| 演算子 | 書式 | 何をする命令? | ポイント |
|---|---|---|---|
| << | a << b | a を b ビット左へずらす | 空きは 0 で埋まる |
| >> | a >> b | a を b ビット右へずらす | unsigned なら 0 埋めが基本 |
複合代入(よく出る)
| 演算子 | 書式 | 意味 |
|---|---|---|
| >>= | x >>= n | x = x >> n と同じ |
| <<= | x <<= n | x = x << n と同じ |
表の説明
- こういう一覧を先に頭に入れると、後の関数が読みやすくなります。
- 特に &= や |= や ^= も現場で頻出ですが、今回は提示文にある >>= を中心に扱います。
count_bits:セットされたビット(1)の個数を数える
何をする関数?
int count_bits(unsigned x);
x の中に 1 がいくつあるか数えて返す関数です。
ビットが 1 の場所は「スイッチがON」みたいなものなので、ON の数を数えるイメージですね。
仕組みを表で分解(提示文①②の整理)
| 手順 | やること | 使う演算 | 意味 |
|---|---|---|---|
| ① | x の最下位ビットが 1 か調べる | x & 1U | 最下位だけ取り出して判定 |
| ② | 調べ終わった最下位ビットを捨てる | x >>= 1 | 右へ1ビットずらして次へ |
表の説明
- 1U は 000...0001 という「最下位ビットだけが 1 のマスク」です。
- x & 1U の結果が 1 なら最下位ビットが 1、0 なら最下位ビットが 0 です。
- 右シフトで次のビットが最下位に来るので、同じ判定を繰り返せます。
図:x=10 のときのカウント
10 は 2進数で 1010 です(ここでは4ビットで表示)。
x = 1010, bits=0
x&1 -> 0 なので増えない
x>>=1 -> 0101
x = 0101, bits=0
x&1 -> 1 なので bits=1
x>>=1 -> 0010
x = 0010, bits=1
x&1 -> 0
x>>=1 -> 0001
x = 0001, bits=1
x&1 -> 1 なので bits=2
x>>=1 -> 0000
x が 0 になったので終了、答えは 2図の説明
- 右にずらしながら、最下位だけ毎回チェックする方式です。
- どんなビット幅でも同じロジックで動きます。
int_bits:unsigned 型が何ビットかを“計算で”求める
何をする関数?
int int_bits(void);
unsigned が何ビットで構成されるかを返す関数です。
提示文の核心はこの一行です。
- ~0U は全ビットが 1 の unsigned 値
- その 1 の個数を数えればビット数が分かる。
図:~0U を得る
0U : 0000...0000
~0U : 1111...1111
図の説明
- 0U は全ビット0です。
- ~ で反転すると全ビット1になります。
- 全ビット1の中に 1 は何個? → それがビット数です。
- だから count_bits(~0U) でビット数が出ます。
print_bits:整数の全ビットを 0 と 1 で表示する
何をする関数?
void print_bits(unsigned x);
x を上位ビットから下位ビットまで 0/1 で表示します。
提示文のこの式がポイントでした。
- ((x >> i) & 1U) で「第 i ビットが 1 か」を判定
第 i ビット判定ができる理由
| 操作 | 目的 | 例(第3ビットを見たい) |
|---|---|---|
| x >> i | 見たいビットを最下位へ移動 | x >> 3 |
| (x >> i) & 1U | 最下位だけ取り出す | (x >> 3) & 1U |
表の説明
- 右シフトで “見たいビット” を最下位に持ってきます。
- そこに 1U マスクで AND すると、最下位だけを取り出せます。
- 1 ならそのビットは 1、0 なら 0 です。
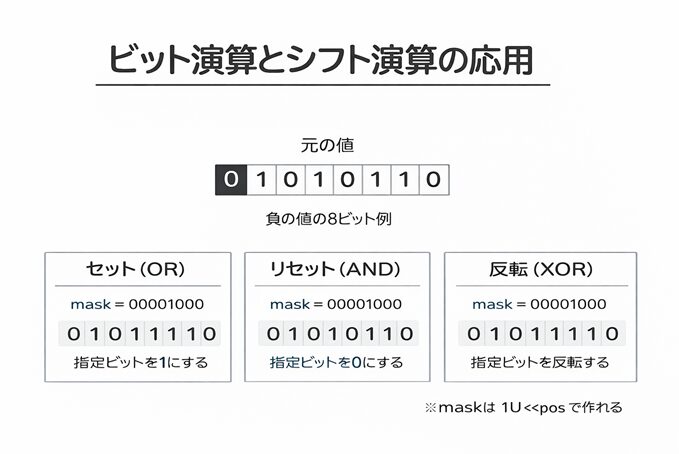
ビット演算の応用:セット/リセット/反転は「マスク」で決まる
ここが応用の一番おいしいところです。
やりたい操作は「特定のビットだけ変えたい」です。そこで マスク(操作対象を決めるビット列)を使います。
基本3操作(提示文の要点)
| やりたいこと | 代表式 | どうしてそうなる? |
|---|---|---|
| セット(1にする) | x | mask | mask が 1 の場所は必ず 1 になる。 |
| リセット(0にする) | x & ~mask | mask が 1 の場所だけ 0 に落とせる。 |
| 反転(トグル) | x ^ mask | mask が 1 の場所だけ反転する。 |
図:最下位ビットだけ操作するマスク
最下位ビットだけを対象にするなら mask は 1U(…0001)です。
mask = 0001
セット : x | 0001
リセット : x & 1110 (~0001 = 1110)
反転 : x ^ 0001
図の説明
- mask の 1 が「操作する場所」です。
- 0 の場所は基本的に「そのまま」になります。
- だから“最下位ビットだけ”が変化します。
サンプルプログラム
第3ビット(0始まりで pos=3)をセット/リセット/反転するプログラムです。
プロジェクト名:chap7-19-1 ソースファイル名:chap7-19-1.c
Visual Studio でこのプログラムを実行するには、SDLチェック設定を変更しておく必要があります。
1.プロジェクト名を右クリックして、「プロパティ」をクリックします。
2.「C/C++」→「全般」→「SDLチェック」を「いいえ」に切り替えて「OK」をクリックします。
// 第posビットをセット/リセット/反転して表示する例
#include <stdio.h>
int count_bits(unsigned x)
{
int bits = 0;
while (x) {
if (x & 1U) bits++;
x >>= 1;
}
return bits;
}
int int_bits(void)
{
return count_bits(~0U);
}
void print_bits(unsigned x)
{
for (int i = int_bits() - 1; i >= 0; i--)
putchar(((x >> i) & 1U) ? '1' : '0');
}
int main(void)
{
unsigned n;
int pos = 3; // 第3ビットを操作(0始まり)
unsigned mask = 1U << pos; // 000...1000
printf("ビット操作の練習:第3ビットを変えてみよう。\n");
printf("非負の整数を入力してください:");
scanf("%u", &n);
putchar('\n');
printf("入力値 = "); print_bits(n); putchar('\n');
printf("第3ビットをセット = "); print_bits(n | mask); putchar('\n');
printf("第3ビットをリセット = "); print_bits(n & ~mask); putchar('\n');
printf("第3ビットを反転 = "); print_bits(n ^ mask); putchar('\n');
return 0;
}このプログラムのポイント解説
- mask = 1U << pos で「操作したいビットだけ 1 のマスク」を作ります。
- セットは n | mask
- リセットは n & ~mask
- 反転は n ^ mask
という“公式”をそのまま当てはめています。
演習問題
ここからは、提示文の「演習 7-2〜7-5」に似た形で、同じ狙いの問題を4つ用意します。
どれも unsigned を前提にして可搬性を上げます。
演習7-2:シフトと 2 のべき乗の一致確認
unsigned x と n を読み込み、x << n と x * (1U << n) が一致すること、x >> n と x / (1U << n) が一致することを表示で確かめるプログラムを作成せよ。
ただし n は 0〜(ビット数-1) の範囲とする。
解答例(要点)
unsigned p = 1U << n;
printf("x<<n = %u\n", x << n);
printf("x*p = %u\n", x * p);
printf("x>>n = %u\n", x >> n);
printf("x/p = %u\n", x / p);解説
- unsigned の左シフトは、オーバーフローしない範囲なら 2^n 倍に一致しやすいです。
- unsigned の右シフトは、2^n で割った商(小数切り捨て)に一致しやすいです。
- ただし上位が弾き出される(オーバーフローする)と一致しません。そこを観察するのが狙いです。
演習7-3:右回転・左回転(ローテート)
unsigned x を右に n ビット回転した値を返す rrotate、左に n ビット回転した値を返す lrotate を作成せよ。
unsigned のビット数は int_bits() を使って求めてよい。
解答例
unsigned rrotate(unsigned x, int n)
{
int w = int_bits();
n %= w;
return (x >> n) | (x << (w - n));
}
unsigned lrotate(unsigned x, int n)
{
int w = int_bits();
n %= w;
return (x << n) | (x >> (w - n));
}解説
- 回転は「シフトで弾き出された部分を反対側に戻す」操作です。
- 右回転なら (x >> n) で右へずらし、弾き出される下位 n ビットは (x << (w-n)) で上位へ回して OR します。
- n を w で割った余りにするのが安全策です(回転量がビット幅を超えないように)。
演習7-4:第 pos ビットのセット/リセット/反転
unsigned x の第 pos ビットをセットした値を返す set、リセットした値を返す reset、反転した値を返す inverse を作成せよ。
解答例
unsigned set(unsigned x, int pos)
{
return x | (1U << pos);
}
unsigned reset(unsigned x, int pos)
{
return x & ~(1U << pos);
}
unsigned inverse(unsigned x, int pos)
{
return x ^ (1U << pos);
}解説
- 1U << pos で “第posビットだけが1” のマスクを作るのが全ての基本です。
- OR で 1 に固定、AND と ~ で 0 に固定、XOR で反転です。
演習7-5
unsigned x の第 pos ビットから第 pos+n-1 ビットまでの n 個を、セット/リセット/反転する関数 set_n / reset_n / inverse_n を作成せよ。
解答例
unsigned make_mask(int pos, int n)
{
// n個の1を作ってposだけ左へ
// 例: n=3 -> 0b111, pos=4 -> 0b1110000
return ((1U << n) - 1U) << pos;
}
unsigned set_n(unsigned x, int pos, int n)
{
unsigned m = make_mask(pos, n);
return x | m;
}
unsigned reset_n(unsigned x, int pos, int n)
{
unsigned m = make_mask(pos, n);
return x & ~m;
}
unsigned inverse_n(unsigned x, int pos, int n)
{
unsigned m = make_mask(pos, n);
return x ^ m;
}解説
- (1U << n) - 1U で下位 n ビットが全部1の形を作れます。
- それを pos だけ左へずらして範囲マスクにします。
- あとは set/reset/inverse の公式に当てるだけです。
- 注意:n がビット幅以上になると 1U << n が危険なので、実用では範囲チェックも入れます。
この記事の要点まとめ
- マスク(操作したいビットが1の値)を作るのが第一歩
- OR でセット、AND と ~ でリセット、XOR で反転
- シフトと組み合わせると、任意位置・任意個数のビットを自在に操作できる。
- unsigned を基本にすると、環境差の罠を踏みにくい。
